Conceptualizing an Autotiler

By rador.dekeche, October 9, 2024

So, you’ve got a tileset you want to use, but you don’t want to manually place every individual tile on the map. Well, that’s where an autotiler comes into play. Simply setup the mapping between the base tileset you want to use, and the autotiler plate, and you’re good to go, right? Until you look at something like this;

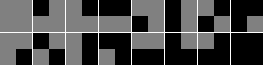
And if you’re not exactly very visually inclined, you might get lost when trying to figure out exactly what you’re looking at, particularly if your tileset wasn’t designed with this sort of setup in mind.

The key thing to understand is that what you’re looking at is not a tileset, but rather a binary sequence. 0 for no adjacency, 1 for upper left, 2 (10) for upper right, 4 (100) for lower left, and 8 (1000) for lower right. With all the other tiles being a combination of the 4 primary adjacencies. And once this connection is made, then it’s simple to understand the underlying concept of how autotilers work. Essentually, autotilers need two things to work; a tile bitmask ID that’s calculated based on tile adjacencies, and an underlying data array that defines those adjacencies. For the above example, we’ve got a simple 4 bit ID setup, which can work with an underlying binary array. When “filling” a tile, we set the tiles location in the underlying array to 1. Then we calculate each tile’s ID based on that tile’s surrounding values in the underlying array. So a tile with one adjacent ‘1’ in the upper left will use the 0001 (1) bitmask id. directly above would use 0011 (3) as the bitmask ID.

Which is just a simple example of how this can work. But you can make this more complicated; increasing the scope to an 8-bit ID means the system can handle adjacencies in all 8 directions. Or, you can add other values to the bitmask. As an example; (##)(####) – the first two bits are a randomized value, where the last 4 bits are the adjacency ID calculated by the autotiling algorithm. Which results in an algorithm that produces maps with some randomness in the actual tiles present, rather than just re-using the same 16 tile for every situation. or (#)(####)(####) could represent a multi-environment tileset. With the first bit selecting what environment the tile is, and the other two bitmasks tracking adjacency for each of the underlying environments. Which could potentially be useful if you use Blob or Wang tiles to produce tilesets with multiple environments and adjacencies to handle.